§ 11. ГРАВИТАЦИОННЫЕ СИЛЫ: ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ

Этот закон, называемый законом всемирного тяготения, в математической форме записывается следующим образом:

где m₁ и m₂ – массы тел, R – расстояние между ними (см. рис. 11а), а G - гравитационная постоянная, равная 6,67^.10^-11 Н^.м²/кг².

Закон всемирного тяготения был впервые сформулирован И. Ньютоном, когда он пытался объяснить один из законов И. Кеплера, утверждающий, что для всех планет отношение куба их расстояния R до Солнца к квадрату периода  T обращения вокруг него одинаково, т.е.

Выведем закон всемирного тяготения так, как сделал это Ньютон, считая, что планеты движутся по окружностям. Тогда по второму закону Ньютона на планету массой m_Пл, движущуюся по окружности радиуса R со скоростью v и центростремительным ускорением v²/R должна действовать сила F, направленная к Солнцу (см. рис. 11б) и равная:

 

Скорость v планеты можно выразить через радиус R орбиты и период обращения T:

Подставляя (11.4) в (11.3) получаем следующее выражение для F:

Из закона Кеплера (11.2) следует, что T² = const^.R³ . Следовательно, (11.5) можно преобразовать в:

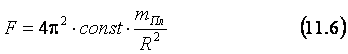
Таким образом, Солнце притягивает планету с силой прямо пропорциональной массе планеты и обратно пропорционально квадрату расстояния между ними. Формула (11.6) очень похожа на (11.1), не хватает лишь массы Солнца в числителе дроби справа. Однако если сила притяжения между Солнцем и планетой зависит от массы планеты, то эта сила должна зависеть также и от массы Солнца, а значит, константа в правой части (11.6) содержит массу Солнца в качестве одного из сомножителей. Поэтому Ньютон выдвинул своё знаменитое предположение, что гравитационная сила должна зависеть от произведения масс тел и закон стал таким, каким мы его записали в (11.1).

Закон всемирного тяготения и третий закон Ньютона не противоречат друг другу. По формуле (11.1) сила, с которой тело 1 притягивает тело 2, равно силе, с которой тело 2 притягивает тело 1.   

Для тел обычных размеров гравитационные силы очень малы. Так, два рядом стоящих легковых автомобиля притягиваются друг к другу с силой, равной весу капли дождя. С тех пор, как Г. Кавендиш в 1798 г. определил значение гравитационной постоянной, формула (11.1) помогла совершить очень много открытий в «мире огромных масс и расстояний». Например, зная величину ускорения свободного падения (g=9,8 м/с²) и радиус Земли (R=6,4^.10⁶ м), можно вычислить её массу m_З следующим образом. На каждое тело массой m₁ вблизи поверхности Земли (т.е. на расстоянии R от её центра) действует гравитационная сила её притяжения, равная m₁g, подстановка которой в (11.1) вместо F даёт:

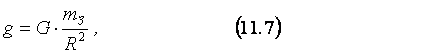
откуда получаем, что m_З = 6^.10²⁴ кг.

Вопросы для повторения:

·        Сформулируйте закон всемирного тяготения?

·        Что такое гравитационная постоянная?

 

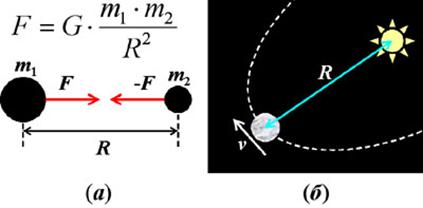
Рис. 11. (а) – к формулировке закона всемирного тяготения; (б) – к выводу закона всемирного тяготения из закона Кеплера.