§ 14. ИМПУЛЬС ТЕЛА. ЗАМКНУТЫЕ СИСТЕМЫ. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА

Пусть сила F начинает действовать на тело m, движущееся со скоростью v₁.  По второму закону Ньютона тело сразу начнёт двигаться с ускорением a=F/m , и через промежуток времени Dt его скорость станет равной v₂=v₁+a^.Dt. При этом будет справедливо следующее равенство:

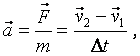
 откуда следует, что

Таким образом, изменение вектора импульса тела, произошедшее за промежуток времени Dt, равно произведению вектора силы на время её действия. При этом вектор импульса изменяется только в том направлении, в котором действует сила.  

До сих пор мы рассматривали движение какого-нибудь одного тела и действие сил на это тело. Часто, однако, приходится рассматривать движение сразу нескольких взаимодействующих тел, например, соударение бильярдных шаров, движение планет солнечной системы или стыковка двух космических аппаратов. В каждом из этих случаев мы изучаем не одно тело, а систему, состоящую из нескольких взаимодействующих между собой тел. При этом существуют такие системы, тела в которых взаимодействуют только между собой, и можно считать, что никакие внешние силы на такие системы не действуют. Такие системы тел называют замкнутыми или изолированными. Солнечную систему можно считать замкнутой системой тел, так как она очень удалена от других космических тел нашей Галактики.

Рассмотрим, как меняется импульс замкнутой системы, состоящей из двух тел – А и Б, при их столкновении. Согласно третьему закону Ньютона, сила F, с которой тело А действует на тело Б, равна по величине и противоположна по направлению силе, с которой тело Б действует на тело А. Поэтому для каждого из тел можно записать уравнение, аналогичное (14.1), где индексы А и Б указывают на то, что оно написано для тел А и Б, соответственно:

Складывая уравнения в (14.2), получаем:

В правой части уравнения (14.3) стоит суммарный импульс системы до столкновения, а в левой – он же, но после. Таким образом, суммарный импульс тел замкнутой системы не изменяется в результате взаимодействия тел этой системы. Этот вывод, справедливый для любых замкнутых систем, называют законом сохранения импульса.

Применим закон сохранения импульса к решению задачи о неупругом столкновении двух шаров, сделанных, например, из пластилина, при условии, что после столкновения они движутся, как единое целое (см. рис. 14а). Считая систему из двух шаров замкнутой, приравниваем значения суммарных импульсов системы до и после столкновения (см. 14.3):

откуда можно легко найти скорость движения v слипшихся шаров после их неупругого столкновения.

Закон сохранения импульса можно использовать для вычисления скорости v₁ отдачи пушки массой m₁ после выстрела снарядом массы m₂ со скоростью v₂ (см. рис. 14б). Система, состоящая из пушки и снаряда, не является замкнутой, т.к. на неё действует сила притяжения Земли. Однако в горизонтальном направлении на эту систему не действуют внешние силы, если пренебречь силами трения. Поэтому, применяя закон сохранения горизонтальной составляющей импульса системы и считая, что импульс системы до выстрела был равен нулю, имеем:

m₁v_1x + m₂v_2x = 0 ,

откуда можно вычислить скорость v_1x отдачи пушки после выстрела.

Вопросы для повторения:

·        Дайте определение импульса тела.

·        Как изменяется импульс тела при действии силы?

·        Какие системы тел называют замкнутыми?

·        Сформулируйте закон сохранения импульса.

 

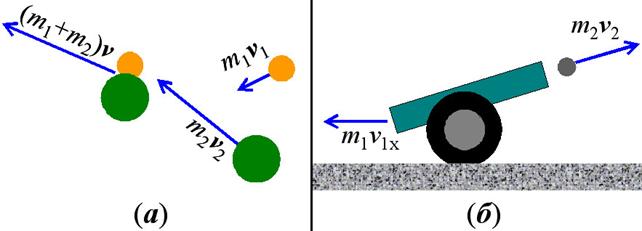
Рис. 14.(а) – к задаче о неупругом столкновении двух пластилиновых шаров; (б) – к вычислению скорости отдачи пушки после выстрела.