§ 16. РАБОТА СИЛЫ. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ ТЕЛА: ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ.

Согласно второму закону Ньютона тело приобретает ускорение в направлении действия силы, и чем дольше будет действовать сила, тем большее перемещение совершит тело в данном направлении. Вклад силы в перемещение s тела (см. рис. 16а) можно оценить, вычисляя величину работы A силы F по данной формуле:

A = F^.s^.cos(a) ,                            (16.1)

где a - угол между векторами F и s. В системе единиц СИ работа измеряется в джоулях (Дж): 1 Дж = 1 Н^.м. Из (16.1) следует, что при p/2<a<3p/2 работа силы отрицательна. При таких значениях a тело движется в одну сторону, а сила действует в другую, тормозя движение тела (рис. 16.б). Сила, действуя на тело, может вообще не совершать работу, если она направлена перпендикулярно его вектору перемещения (рис. 16в). Если проекция силы в направлении перемещения, F_S изменяется, то величину работы можно вычислять, измеряя площадь под кривой зависимости F_S от s, аналогично тому, как мы измеряли путь в §3.

Энергией называют способность тела или системы тел совершить работу. Ветер, надувая парус, движет лодку вперёд и совершает работу, а значит, движущийся воздух обладает энергией. Сжатая пружина имеет энергию, т.к. распрямляясь, совершает работу, приводя в движение механизм часов. Движущийся бильярдный шар тоже обладает энергией, т.к. при столкновении с неподвижным, действует на него с силой, совершая работу. Во всех этих случаях состояние тел, обладающих энергией, после того, как они совершили работу над другими телами, менялось: воздух рядом с парусом замедлялся, пружина часов распрямлялась, а движущийся бильярдный шар терял скорость после столкновения с неподвижным.

Механической энергией тел называют энергию, связанную с их скоростями и относительным положением. Чем больше скорость тела, тем большей энергией оно обладает. Энергию, связанную со скоростью тела, называют его кинетической энергией, E_К. Сжатая пружина, хоть и неподвижна, но обладает энергией, т.к., распрямившись, может совершить работу. То же можно сказать и о приподнятом над землёй мяче, т.к., если его отпустить, то он, разогнавшись и ударившись обо что-нибудь, совершит работу, а значит даже сначала, когда он ещё не двигался, он уже обладал энергией. Такую энергию, связанную только с относительным расположением тел или их частей (деформацией), называют потенциальной энергией, E_П. Таким образом, механическая энергия тела или системы тел равна сумме их потенциальных и кинетических энергий.

Вычислим работу, которую совершает сила F, разгоняя неподвижное тело массы m до скорости v (см. рис. 16г). Действие силы приведёт к тому, что тело будет двигаться с ускорением a=F/m. Тело достигнет скорости v через промежуток времени t=v/a, пройдя при этом путь s=at²/2. Поэтому работа A, совершённая силой F, составит:

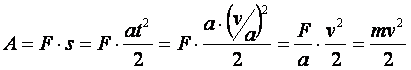
Аналогично, если на тело, движущееся со скоростью v, начинает действовать сила, тормозящая его, то это тело успеет до полной остановки совершить работу, равную mv²/2. Таким образом, кинетическая энергия тела, E_К равна:

E_К = mv²/2.                                  (16.2)

 Найдём потенциальную энергию тела массы m, приподнятого на высоту h над поверхностью земли (см. рис. 16д). Если дать этому телу свободно падать, то оно начнёт двигаться с ускорением свободного падения g и, как легко показать, у поверхности земли будет иметь скорость v=(2gh)^1/2. Поэтому у поверхности земли тело будет обладать кинетической энергией, равной mv²/2, и остановившись, сможет совершить такую же по величине работу. Значит, находившись на высоте h над землёй, тело обладало потенциальной энергией, E_П, равной:

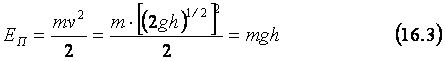
Вопросы для повторения:

·        Дайте определения работы силы и энергии.

·        Как кинетическая энергия зависит от скорости тела?

·        Чему равна потенциальная энергия приподнятого тела?

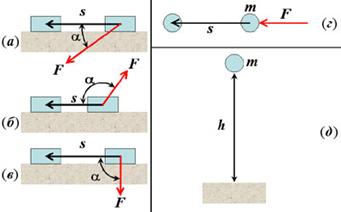
Рис. 16. (а), (б) и (в) – к вычислению работы силы для разных углов a; (г) и (д) – к вычислению кинетической и потенциальной энергии, соответственно.