§ 17. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ В ЗАМКНУТОЙ СИСТЕМЕ. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ

Консервативными называют те силы, работа которых по любой замкнутой траектории равна нулю. Сила тяжести являются одной из консервативных сил. На рис. 17а показана замкнутая траектория в вертикальной плоскости в виде прямоугольника (1-2-3-4), вдоль которой вычислена суммарная работа силы тяжести, оказавшаяся равной нулю. Сила трения скольжения может служить примером неконсервативной силы, так как её работа по замкнутому контуру никогда не равна нулю.

Силы упругости тоже являются консервативными. Докажем это для пружины, перемещающей тело по гладкой поверхности без трения (см. рис. 17б). Согласно закону Гука (см. §13) сила F, с которой растянутая пружина действует на тело, равна k^.s, где k – коэффициент упругости пружины, а  s – её удлинение относительно недеформированного состояния. При перемещении тела из s=s₀ до s=0 проекция силы на вектор перемещения, k^.s, совершит работу A_s0-0, величина которой равна площади заштрихованного треугольника под графиком на рис. 17б. Поэтому A_s0-0=k^.s₀²/2 . При обратном движении тела (от s=0 до s=s₀) на каждом отрезке пути проекция силы на вектор перемещения будет отрицательна, -k^.s , и совершённая работа A_0-s0= -k^.s₀²/2. Таким образом,

A_s0-0 + A_0-s0 = 0,

и упругие силы пружины можно считать консервативными.

Доказывая консервативность сил упругости пружины, мы вывели формулу для вычисления работы, которую может совершить растянутая пружина, определив, таким образом, как зависит потенциальная энергия, E_П пружины от величины деформации s₀:

E_П = k^.s₀²/2.                        (17.1)

Проверим теперь, соблюдается ли закон сохранения механической энергии для тела массы m, падающего под действием силы тяжести (см. рис. 17в). Пусть, в момент времени t=0 тело, находясь на высоте на высоте H над землёй, неподвижно, а значит, его кинетическая энергия, E_К =0. Потенциальная энергия тела, как следует из (16.3), составляет E_П = mgH. Таким образом, механическая энергия тела, равная сумме кинетической и потенциальной, сначала (t=0) равна mgH. Когда тело, падая, окажется на высоте h над землёй, его потенциальная энергия уменьшится на mg^.(H-h) и станет равной mgh, а кинетическая составит mv²/2, где v-скорость тела на данной высоте. Найдём v, считая, что тело падало с ускорением свободного падения, g.

Если считать, что падающее тело достигло высоты h через время t полёта, то его скорость v на данной высоте должна быть v=gt. С другой стороны, для пути, пройденного падающим телом, справедливо, что H-h=gt²/2 . Таким образом, можно найти, что скорость v тела на высоте h над землёй равна v=(2g(H-h))^1/2. Подставляя это значение скорости в выражение для кинетической энергии тела, получаем:

E_К = mg^.(H-h),

откуда следует, что кинетическая энергия падающего тела увеличилась на столько же, на сколько уменьшилась его потенциальная энергия. Таким образом, механическая энергия падающего без трения тела остаётся постоянной в течение его полёта.

В условиях, когда силы взаимодействия между телами включают в себя и неконсервативных сил (например, силу трения), механическая энергия замкнутой системы постепенно уменьшается. Однако энергия никогда не исчезает бесследно. Она лишь переходит в другие формы – тепловую (тела нагреваются), химическую (образуются новые вещества), электрическую (разделяются электрические заряды) и др.

Заканчивая изучение механики, заметим, что существует ещё один очень важный закон, объединяющий все те, с которыми мы уже знакомы. Это – принцип относительности Галилея, утверждающий, что все механические процессы протекают одинаково в любых инерциальных системах отсчёта. Так, закон сохранения механической энергии действует и на суше и на корабле поступательно, равномерно и прямолинейно плывущем по морю. Наоборот, в неинерциальных системах многие законы механики становятся несправедливыми.

Вопросы для повторения:

·        Что такое консервативные силы? Приведите примеры.

·        Сформулируйте закон сохранения механической энергии.

·        Сформулируйте принцип относительности Галилея.

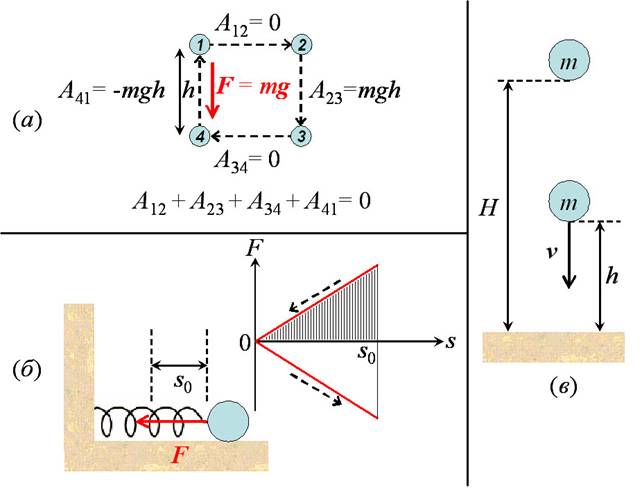
Рис. 17. (а) - вычисление работы силы тяжести по замкнутой траектории в вертикальной плоскости; (б) - к доказательству консервативности упругой силы пружины; (в) – к справедливости закона сохранения энергии для падающего тела.