§ 24.  УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ЗАКОН АВОГАДРО

В §23 мы вывели формулу, связывающую давление идеального газа, p, концентрацию молекул в нём, n, и его абсолютную температуру, Т:

p = nkT  ,                                    (24.1)

где k – постоянная Больцмана. Однако в большинстве случаев пользоваться формулой (24.1) неудобно, т.к. величина n, как правило, неизвестна, а мы лишь знаем, какой это газ и какой объём он занимает. Чтобы в этих случаях формулой (24.1) было пользоваться проще, преобразуем её следующим образом. Пусть газ, состоящий из N молекул, находится в сосуде объёмом V. Тогда концентрация, n молекул равна:

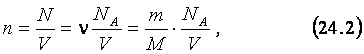
где m и n - масса и количество вещества, содержащееся в газе с молярной массой M и объёмом V, а  N_A – число Авогадро (см. 19.1 и 19.2). Подставляя (24.2) в (24.1), получаем:

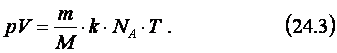
Произведение kN_A обозначают буквой R и называют универсальной (молярной) газовой постоянной, которая равна 8,31 Дж/(моль^.К). Заменяя kN_A на R в формуле (24.3), получаем:

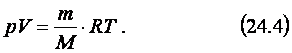
Уравнение (24.4) называют уравнением состояния идеального газа или уравнением Менделеева-Клапейрона, названным в честь русского учёного Д.И. Менделеева и французского физика Б. Клапейрона. Формула (24.4) определяет взаимозависимость трёх макроскопических характеристик данной массы газа, определяющих его состояние, – давления, объёма и температуры.

Уравнение Менделеева-Клапейрона позволяет вычислить одну из пяти переменных (p, V, m, M и T), если значения остальных четырёх известны. Можно, например, найти молярную массу, М газа, т.е. определить его относительную молекулярную массу, если измерить его давление, объём, массу и температуру.

Из уравнения (24.4) следует, что если данная масса газа находится в состоянии 1, в котором её давление, объём и температуры равны p₁, V₁ и T₁, соответственно, а потом переходит в состояние 2 (см. рис. 24а), в котором её давление, объём и температуры становятся равными p₂, V₂ и T₂, то: 

Уравнение (24.5), называемое уравнением Клапейрона, позволяет вычислить значение одной из макроскопических характеристик газа в состоянии 2, если остальные две известны.

 Возьмём одинаковое число молей n двух разных газов (А и Б). Пусть эти газы имеют одинаковую температуру T₀ и давление p₀. Тогда из уравнения (24.4) следует, что объёмы этих газов, V_А и V_Б, тоже равны:

Таким образом, при одинаковых давлении и температуре равные объёмы различных газов содержат одинаковое количество вещества, т.е. молекул. Этот вывод называют законом Авогадро. Из закона Авогадро и формулы (24.6) следует, что при нормальных условиях, т.е. при температуре 0^оС (Т₀=273 К) и нормальном атмосферном давлении (p₀=101325 Па), газ, взятый в количестве 1 моль, занимает объём 0,0224 м³ или 22,4 литра (см. рис. 24б).

Вопросы для повторения:

·        Сформулируйте уравнение Менделеева-Клапейрона. Для каких газов оно справедливо?

·        Как связана универсальная газовая постоянная с постоянными Больцмана и Авогадро?

·        Сформулируйте закон Авогадро.

·        Какие объёмы занимает один, два и три моля идеального газа при нормальных условиях?

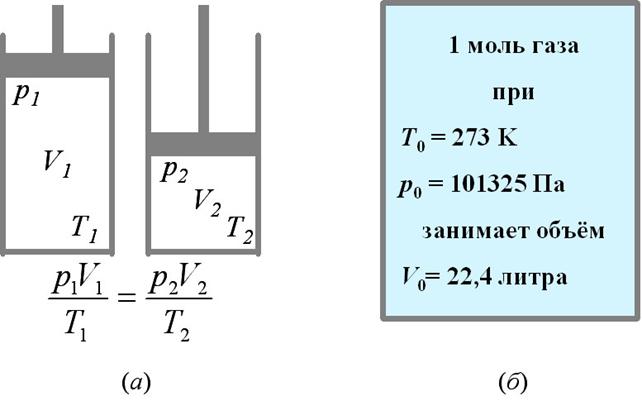
Рис. 24. (а) – связь между параметрами газа в двух его состояниях; (б) – связь между параметрами одного моля газа при нормальных условиях.