§ 3. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ: УРАВНЕНИЕ И ГРАФИК

При равномерном движении путь, пройденный телом, например, за любую одну секунду в два раза меньше, чем путь, пройденный этим же телом за любые две секунды. Примером равномерного движения может служить движение автомобиля на прямом участке загородного шоссе, если водитель поддерживает неизменной частоту оборотов двигателя. Равномерно движется поезд, преодолевая длинный ровный перегон между станциями.

Так как скорость (см. § 2) равна отношению перемещению тела к промежутку времени, за который это перемещение пройдено, то при равномерном движении она будет постоянной. Чтобы вывести уравнение прямолинейного равномерного движения, предположим, что тело движется вдоль оси Ox со скорость v в положительном направлении и в момент времени t=0 его координата равна x₀. Через время t координата тела станет равной x, а проекция вектора перемещения тела за это время, составит x-x₀. Согласно определению скорости, можно записать следующее уравнение:             

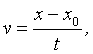
откуда после несложных преобразований получаем следующее уравнение, связывающее координату тела x и время t при равномерном и прямолинейном движении с проекцией скорости v :

x = x₀ + vt ,                                   (3.1)

Построим график зависимости перемещения тела от времени для прямолинейного равномерного движения, полагая x₀ = 1 м, v = 2 м/с. Как видно на рис.3 (верх, чёрная прямая), графиком движения является прямая линия. Графиком прямолинейного равномерного движения всегда является прямая линия. Чем больше скорость равномерного движения, тем круче прямолинейный график зависимости перемещения тела от времени (см. красную прямую для v = 6 м/с).

Графики прямолинейного движения можно строить и для случаев, когда тело движется равномерно в течение определённого промежутка времени, а затем движется равномерно, но с другой скоростью в течение другого промежутка времени, затем снова меняет скорость и т.д. (см. отрезки АВ, ВС на рис. 3, верх).

Подобно графику изменению координаты точки, можно построить и график зависимости скорости от времени. По оси ординат отложим значения скорости, а по оси абсцисс – время (см. рис. 3, низ). Так как скорость равномерного движения постоянна, то её график будет прямой линией, параллельной оси времени. Чем больше скорость движения, тем выше над осью абсцисс будет её график, и наоборот (см. отрезки АВ, ВС на рис. 3, низ).

Площадь прямоугольника, заштрихованного на рисунке 3 (низ), равна произведению отрезка, изображающего скорость v, на отрезок, изображающий промежуток времени t, т.е равна vt или длине пройденного за это время пути. Значит, путь, пройденный за какой-либо интервал времени, численно равен площади части фигуры между осью времени и графиком скорости от времени, ограниченной двумя вертикальными отрезками, проведёнными из начала и конца этого промежутка времени.   

Вопросы для повторения:

·        Какая линия на графике зависимости координаты тела от времени соответствует прямолинейному равномерному движению?

·        Какая линия на графике зависимости скорости тела от времени соответствует прямолинейному равномерному движению?

·        Как связаны между собой скорость движения тела и наклон прямой на графике зависимости координаты тела от времени?

·        Как связаны между собой пройденный путь и площадь под кривой зависимости скорости тела от времени?

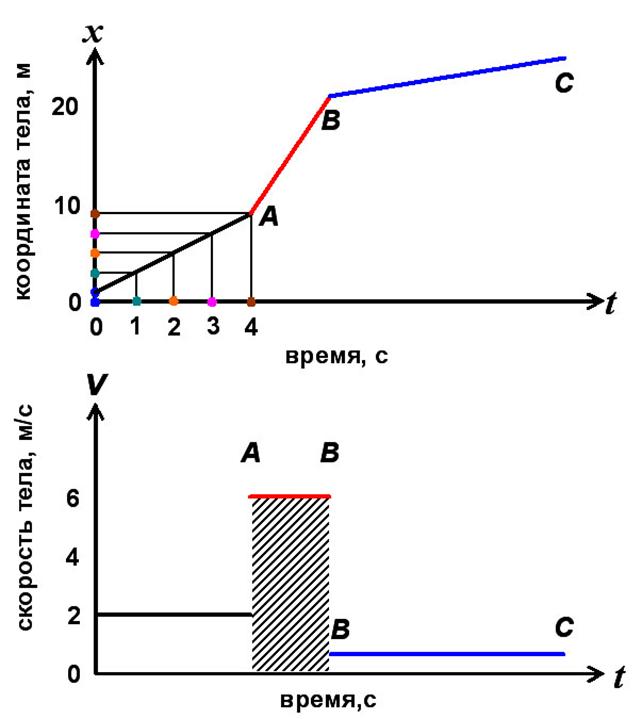
Рис.3. Зависимость координаты тела (верх) и его скорости (низ) от времени при равномерном и прямолинейном движении со скоростью 2 м/с на участке 0A, 6 м/с – AB и 0,66 м/с – BC.