§ 38.  КОНДЕНСАТОРЫ: ЭЛЕКТРОЁМКОСТЬ, ЭНЕРГИЯ.

Пусть проводники А и Б разделёны диэлектриком и первоначально не заряжены. Если перенести с одного из них на другой некоторый заряд q, то эти проводники зарядятся разноимёнными, но одинаковыми по модулю зарядами (рис. 38а). Таким образом, любые два проводника можно сделать системой для хранения и накопления электрического заряда. Систему из двух проводников (обкладок), разделённых тонким слоем диэлектрика, способную хранить электрические заряды значительной величины, называют конденсатором.

Заряд, находящийся на каждой обкладке конденсатора, создаёт между ними электрическое поле, напряжённость которого пропорциональна величине этого заряда, q. Поэтому работа по перенесению любого заряда между обкладками конденсатора, а значит, и напряжение между его обкладками будет пропорциональна заряду q. Таким образом, заряд  q любого конденсатора должен быть пропорционален напряжению U между его обкладками, что можно записать следующим образом:

q = CU  ,                           (38.1)

где С – постоянный для данного конденсатора коэффициент, называемый электроёмкостью конденсатора и равный отношению заряда одной из его обкладок к напряжению между этой обкладкой и другой. Электроёмкость конденсатора не зависит от заряда на его обкладках и определяется только размерами, формой и относительным расположением этих обкладок.

Единицей электроёмкости в СИ является фарад (Ф), названный так в честь М. Фарадея. Конденсатор имеет электроёмкость  в 1 Ф,  если напряжение между его обкладками, обладающими разноимёнными зарядами по 1 Кл, равно 1 В. Из (38.1) следует, что 1 Ф = 1 Кл/1 В. Электроёмкость реальных конденсаторов гораздо меньше 1 Ф, поэтому для её измерения часто используются микрофарад (мкФ, 10^-6 Ф) или пикофарад (пФ, 10^-12 Ф).

Конденсатор, у которого обкладками являются плоские, параллельные друг другу, металлические пластины, разделённые тонким слоем диэлектрика, называют плоским конденсатором (рис. 38б). Электрическое поле между пластинами плоского конденсатора однородное, что позволяет найти следующее вы ражение для электроёмкости С плоского конденсатора:

где S – площадь каждой из пластин, d – расстояние между ними, а e - диэлектрическая проницаемость слоя диэлектрика, разделяющего эти пластины. Таким образом, электроёмкость плоского конденсатора прямо пропорциональна площади его обкладок, диэлектрической проницаемости среды между ними и обратно пропорциональна расстоянию между ними.

Большинство конденсаторов, используемых в различных радиоэлектронных и технических устройствах, по своей конструкции напоминают плоские конденсаторы. Пластинами в них служат две полоски алюминиевой фольги, разделенные тонким слоем диэлектрика: парафинированной бумаги, слюды, воздуха и т.п. По типу используемого диэлектрика конденсаторы называют бумажным, слюдяным, воздушным и т.п. Самой большой электроёмкостью обладают электролитические конденсаторы, в которых изолирующим слоем диэлектрика является тончайшая плёнка оксида алюминия, образующаяся на алюминиевой фольге, помещённой в электролит.

При переносе заряда с одной обкладки на другую совершается работа, которая переходит в потенциальную энергию W_П конденсатора. Очевидно, что энергия заряженного конденсатора зависит от величины заряда q и напряжения U между его обкладками. Эту зависимость, одинаковую для всех видов конденсаторов, легко вывести для плоского конденсатора, между пластинами которого имеется однородное поле напряжённостью Е (рис. 38в). Вклад обеих пластин в суммарное электрическое поле одинаков, и значит, напряжённость электрического поля, создаваемая каждой пластиной, равна Е/2. Чтобы перенести заряд q с пластины А на пластину Б, в поле напряжённостью E/2 на расстояние d, надо совершить работу W_П =qEd/2. Так как U=Ed (см. §37), то W_П =qU/2. Учитывая (38.1), получаем следующее выражение для энергии заряженного конденсатора:

Вопросы для повторения:

·        Что называют конденсатором и его электроёмкостью?

·        От чего зависит электроёмкость плоского конденсатора?

·        Как зависит энергия конденсатора от величин заряда и напряжения между его обкладками?

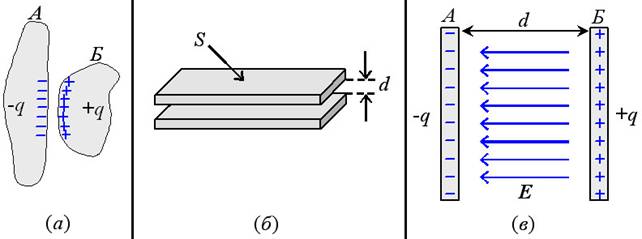
Рис. 38. (а) – схематическое изображение конденсатора; (б) – к вычислению электроёмкости плоского конденсатора по формуле (38.2); (в) – к выводу формулы (38.3) для энергии плоского конденсатора.