§ 5. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ С ПОСТОЯННЫМ УСКОРЕНИЕМ: УРАВНЕНИЕ ДЛЯ СКОРОСТИ И ПРОЙДЕННОГО ПУТИ

Примером ускоренного движения может быть падение цветочного горшка с балкона невысокого дома. В начале падения скорость горшка равна нулю, но за несколько секунд она успевает вырасти до десятков м/с. Примером замедленного движения является движение камня, брошенного вертикально вверх, скорость которого сначала большая, но потом постепенно уменьшается до нуля в верхней точке траектории. Если пренебречь силой сопротивления воздуха, то ускорение в обоих этих случаях будет одинаково и равно ускорению свободного падения, которое всегда направлено вертикально вниз, обозначается буквой g  и равно примерно 9,8 м/с².

 Ускорение свободного падения, g вызвано силой притяжения Земли. Эта сила ускоряет все тела, движущиеся по направлению к земле, и замедляет те, которые движутся от неё.

 Чтобы найти уравнение для скорости при прямолинейном движении с постоянным ускорением, будем считать, что в момент времени t=0 тело имело начальную скорость v₀. Так как ускорение a постоянно, то для любого момента времени t справедливо следующее уравнение:

где v – скорость тела в момент времени t, откуда после нетрудных преобразований получаем уравнение для скорости при движении с постоянным ускорением:

v = v₀ + at                               (5.1)

 Чтобы вывести уравнение для пути, пройденного при прямолинейном движении с постоянным ускорением, построим сначала график зависимости скорости от времени (5.1). Для a>0 график этой зависимости изображён слева на рис.5 (синяя прямая). Как мы установили в §3, перемещение, совершённое за время t, можно определить, если вычислить площадь под кривой зависимости скорости от времени между моментами t=0 и t. В нашем случае фигура под кривой, ограниченная двумя вертикальными линиями t=0 и t, представляет собой трапецию OABC, площадь которой S, как известно, равна произведению полусуммы длин оснований OA и CB на высоту OC:

 Как видно на рис.5, OA = v₀, CB= v₀ + at, а OC = t. Подставляя эти значения в (5.2), получаем следующее уравнение для перемещения S, совершённого за время t при прямолинейном движении с постоянным ускорением a при начальной скорости v₀ :

Легко показать, что формула (5.3) справедлива не только для движения с ускорением a>0, для которого она была выведена, но и в тех случаях, когда a<0. На рис.5 справа красными линиями показаны графики зависимости S при положительных (верх) и отрицательных (низ) значениях a, построенные по формуле (5.3)  для различных величин v₀. Видно, что в отличие от равномерного движения (см. рис. 3), график зависимости перемещения от времени является параболой, а не прямой, показанной для сравнения пунктирной линией.

Вопросы для повторения:

·        Является ли движение с постоянным ускорением равномерным?

·        Дайте определение равноускоренного и равнозамедленного движения.

·        Чему равно ускорение свободного падения, и чем оно вызвано?

·        По какому закону изменяется скорость при равноускоренном или равнозамедленном движении?

·        Как зависит перемещение при равноускоренном движении от времени, ускорения и начальной скорости?

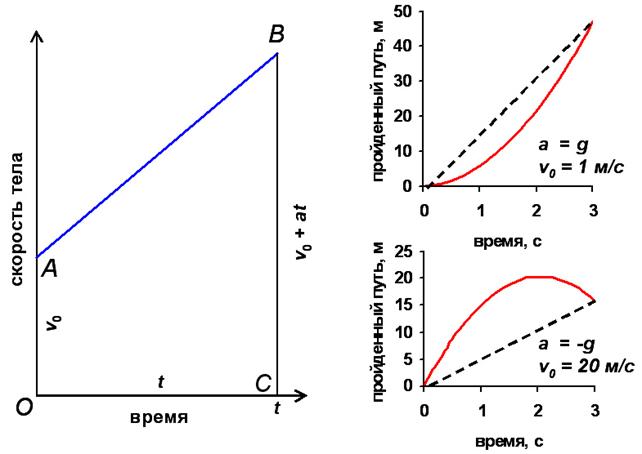
Рис. 5. Слева – зависимость скорости от времени (синяя прямая) при равноускоренном движении; справа – зависимости перемещения от времени (красные кривые) при равноускоренном (верх) и равнозамедленном движении (низ).