§ 6. РАВНОМЕРНОЕ ДВИЖЕНИЕ ПО ОКРУЖНОСТИ: ЦЕНТРОСТРЕМИТЕЛЬНОЕ УСКОРЕНИЕ.

Любое движение по криволинейной траектории происходит с ускорением, так как вектор скорости, направленный по касательной к траектории, меняет своё направление со временем. Примерами криволинейного движения могут служить движение планет вокруг Солнца и электронов вокруг атомного ядра. По криволинейной траектории движется автомобиль, поворачивающий на перекрёстке, и самолёт, заходящий на посадку.

Простейшим криволинейным движением является равномерное движение по окружности, при котором модуль скорости остаётся постоянным, а его направление меняется. Чтобы найти величину и направление вектора ускорения при равномерном движении по окружности с центром в точке О, отметим на ней две близко расположенные точки A и B (см. верх рис. 6, слева). Пусть, в точке А тело было в момент времени t, а в точке В – в момент времени t+Dt. На том же рисунке выходящими из точек А и В нарисованы векторы v_A и v_B, соответствующие скоростям тела в данных точках.

Ускорение a, как известно (см. § 4), равно отношению изменения вектора скорости Dv, произошедшего за интервал времени Dt, к величине этого интервала, откуда следует, что Dv =a^.Dt. В нашем случае Dv = v_A - v_B. Справа вверху на рис.6 показано, как, используя правило треугольника, найти Dv по известным v_A и v_B. При сближении точек Б и А направление  приближается к направлению, перпендикулярному к , а значит  становится направленным к центру окружности, по которой движется тело. Такое движение называют движением с центростремительным ускорением.

Так как v_A и v_B перпендикулярны ОА и ОВ, соответственно, а модули v_A и v_B равны между собой, то треугольники ОАВ и О’A’B’ подобны, как равнобедренные треугольники с равными углами (см. верх рис.6). Поэтому справедливо следующее отношение между длинами сторон этих треугольников:

Для близко расположенных точек А и В длину отрезка АВ можно считать равной длине соответствующей дуги АВ окружности, а длина этой дуги окружности равна произведению модуля скорости, v на Dt. Подставляя в (6.1) A’B’ = a^.Dt , АВ = v^.Dt,    О’A’ = v, ОА = R (радиус окружности), получаем после несложных преобразований следующее выражение для величины центростремительного ускорения:

Любое криволинейное движение на коротких участках траектории всегда можно рассматривать как движение по малой дуге окружности с радиусом, более всего подходящим для данного участка траектории (см. R₁, R₂ и R₃ в нижней части рис.6). Этот радиус называют радиусом кривизны траектории в данной её точке. Если тело движется равномерно (модуль скорости, v не изменяется) по криволинейной траектории, то по формуле 6.2 и известным радиусам кривизны можно вычислить центростремительное ускорение, направленное к центру кривизны траектории в любой её точке.  

Так как вектор центростремительного ускорения всегда направлен перпендикулярно касательной к траектории, то направление вектора ускорения при криволинейном движении никогда не совпадает с направлением касательной к траектории. Поэтому вектор ускорения в этих случаях представляют в виде суммы двух взаимно перпендикулярных составляющих: тангенциальной, a_т (направленной по касательной к траектории) и нормальной, a_н (направленной перпендикулярно к касательной). При этом a_т соответствует изменению модуля скорости движения, а a_н – изменению направления его вектора.

Вопросы для повторения:

·        Куда направлено центростремительное ускорение, и как оно зависит от скорости и радиуса окружности?

·        Чему равны модули тангенциального и нормального ускорения при равномерном движении по окружности?

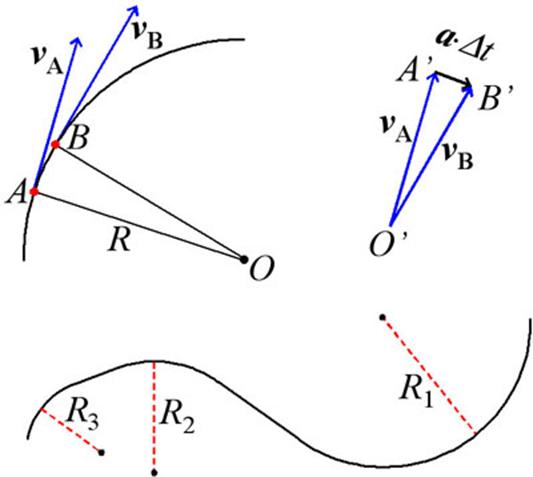
Рис. 6. Верх – к выводу формулы для центростремительного ускорения; низ – криволинейная траектория, несколько участков которой можно заменить дугами окружностей обозначенных радиусов.